Introduction to QCAT

Index: Control allocation; Notation and terminology; QP formulation; Implemented solvers; Toolbox overview; Get started

CONTROL ALLOCATION

The control allocation problem is that of distributing a desired total control effort among a redundant set of actuators. In flight control, for example, the total control effort corresponds to the aerodynamic moments (and sometimes also forces) to be produced, and the actuators are the control surfaces available on the aircraft.

NOTATION AND TERMINOLOGY

We will refer to the total control effort as the virtual control input, v(t), while the actuator positions constitute the true control input, u(t). The total control effort produced by the actuators is decided by the control effectiveness matrix, B:

v(t) = B u(t)

Here, dim(v) = k, dim(u) = m, and B is a (k x m)-matrix.

Each actuator is assumed to be physically limited by upper and lower position and rate limits. Using a digital controller, the rate constraint can be viewed as a time-varying position constraint ("how far can the actuator move during the next sampling interval?"). This gives the following overall box constraint:

umin(t) <= u(t) <= umax(t)

Combining the equations, we see that different commanded values of v(t) lead to different cases - there can either be an infinite set of solutions u(t), one unique solution, or no feasible solution at all.

QP FORMULATION

In the quadratic programming approach to control allocation, also known as l2-optimal control allocation, the control allocation problem is posed as the following sequential least-squares (sls) problem:

min ||Wu(u-ud)|| subj. to u in M

M = arg min ||Wv(Bu-v)|| subj. to umin <= u <= umax

This optimization problem should be interpreted as follows: Given M, the set of feasible control inputs that minimize Bu-v (weighted by Wv), pick the control input that minimizes u-ud (weighted by Wu).

Above, ud is the desired control input (typically zero) and Wu and Wv are weighting matrices. Wu affects the control distribution among the actuators and Wv affects the prioritization among the virtual control components when Bu=v cannot be attained due to the actuator constraints.

The problem can be reformulated as a weighted least-squares (wls) problem:

min ||Wu(u-ud)||^2 + gamma ||Wv(Bu-v)||^2 subj. to umin <= u <= umax

As gamma goes to infinity, the two formulations have the same optimal solution, u(t).

IMPLEMENTED SOLVERS

Six different solvers have been implemented:

SLS

Active set solver for the sequential least-squares formulation above. Determines the optimal solution in a finite number of iterations. Based on

O. Härkegård. Efficient active set algorithms for solving constrained least squares problems in aircraft control allocation. In IEEE CDC, 2002.

WLS

Active set based solver for the weighted least-squares formulation. Determines the optimal solution in a finite number of iterations. Based on the same reference. This solver is also available as a C MEX-file.

MLS

Active set based solver for the sls problem reformulated as a minimal least-squares problem. This requires Wu to be diagonal. Based on

P. Lötstedt. Solving the minimum least squares problem subject to bounds on the variables. BIT, 24:206-224, 1984.

IP

Interior point solver for the wls formulation. Converges uniformly to the optimum in the number of iterations. Contributed by John Petersen, based on

J.A.M. Petersen and M. Bodson. Constrained Quadratic Programming Techniques for Control Allocation. In IEEE CDC, 2003.

CGI

Heuristic method based on cascading generalized inverses (or redistributing pseudoinverses) for the sls formulation. Requires only a finite number of iterations but does not guarantee that the optimal solution is found. Based on

K.A. Bordignon. Constrained Control Allocation for Systems with Redundant Control Effectors. PhD thesis, Virginia Tech, 1996

J.C. Virnig and D.S. Bodden. Multivariable control allocation and control law conditioning when control effectors limit. In AIAA GNCC, 1994.

FXP

Fixed-point interation algorithm for the wls formulation. Converges to the optimal solution as the number of iterations goes to infinity. Based on

J.J. Burken et al. Two reconfigurable flight-control design methods: Robust servomechanism and control allocation. Journal of Guidance, Control, and Dynamics, 24(3):482-493, 2001.

TOOLBOX OVERVIEW

The toolbox functions are grouped into different categories:

QP allocation

Contains the core functions of the toolbox - Matlab implementations of the five solvers listed above. These functions solve the allocation problem for a single virtual control input v, given B, umin, umax, and (optionally) the tuning variables Wv, Wu and ud.

These functions have been implemented as efficiently as possible (to the author's ability).

Direct allocation

For comparison, a simple algorithm for direct allocation has also been implemented (not optimized for speed). The solver is based on the LP formulation presented in

M. Bodson. Evaluation of optimization methods for control allocation. Journal of Guidance, Control, and Dynamics, 25(4):703-711, 2002.

Dynamic allocation

In dynamic control allocation, a term that penalizes the actuator rates is added to the objective function. The resulting frequency dependent control distribution can be computed using the dca command. See also

O. Härkegård. Dynamic control allocation using constrained quadratic programming. In AIAA Guidance, Navigation, and Control Conf., 2002.

Simulation

These functions simulate the time response of different types of allocators to arbitrary inputs (much like the standard LSIM command). They also output the computation time per sample for the selected solver, averaged over a number of repetitions set by the user. The qcatlib Simulink library contains blocks for QP and dynamic control allocation.

Linear control

Features two conversion functions for extracting the control allocation part of a given LQ controller, and for merging an allocator with an LQ controller, respectively. See

O. Härkegård. Resolving actuator redundancy - control allocation vs. linear quadratic control. In European Control Conf., 2003.

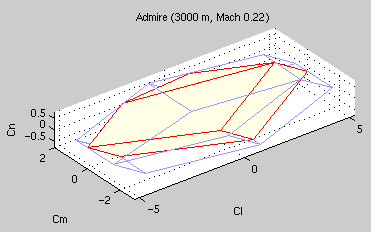
The vview function allows the user to evaluate the gain of using constrained control allocation rather than a linear allocation control law (as in LQ, for example). This is done by visualizing the feasible virtual control set. Screenshot from vview_demo:

Other

Collection of various utility functions.

Aircraft data

Matlab data files containing test data (B, v, plim, rlim, T, t) for two different aircraft models:

The Admire model (used extensively in my PhD thesis).
F-18 related data from
W.C. Durham and K.A. Bordignon. Multiple control effector rate limiting. Journal of Guidance, Control, and Dynamics, 19(1):30-37, 1996.
This is the data set that was used in
O. Härkegård. Efficient active set algorithms for solving constrained least squares problems in aircraft control allocation. In IEEE CDC, 2002.
for evaluating some of the solvers listed above.

GET STARTED

To get started using the toolbox, try the Simulink demos in qcatlib or the examples in the help texts of qp_sim, dir_sim, dyn_sim, and dca. You can also run vview_demo.